Publications (by subject, in reverse chronological order,
with selected abstracts)
Files in pdf format can be read
using the free Adobe Acrobat Reader, which can be downloaded
here.
Files in ps format can be read by any standard Postscript reader.
Geometric group theory
- (with E. Berkove, S. Dharia, and R. McGuigan) The l2-cohomology of
clean complexes, preprint, 2016.
A clean complex is a graph of spaces whose vertex and
edge spaces are graphs and whose attaching maps are embeddings. Clean
complexes are notable because they provide a 2-dimensional test case for virtually special cube complexes. Given an oracle for computing in
U(Fn), we present an algorithm for calculating the l2-homology of
many clean complexes, including all rosy complexes (clean complexes
whose underlying graphs and vertex spaces are n-leave roses). As a result,
we obtain large classes of examples whose Betti numbers do not vanish and do
not depend only on the Euler characteristic.
- (with D. T. Wise) Cubulating malnormal amalgams, Invent. Math. 199
(2015), no. 2, 293-331.
In this paper we examine sufficient conditions on a group G
splitting as a graph of groups that ensure that G acts properly on a CAT(0)
cube complex. The precise conditions are somewhat technical, but they include
hyperbolicity of G relative to abelian subgroups, quasiconvexity of the
vertex groups, and malnormality and subgroup separability properties of the
edge groups. An additional condition involves an extension property for
codimension-1 subgroups. Many of the conditions are satisfied automatically
when the edge groups are free, or maximal cyclic.
- (with D. T. Wise) Cubulating graphs of free groups with cyclic edge
groups, Amer. J. Math. 132 (2010), no. 5, 1153-1188.
We prove that if G is a finitely generated group that splits
as a graph of free groups with cyclic edge groups, and G has no
non-Euclidean Baumslag-Solitar subgroups, then G is the fundamental group
of a compact nonpositively curved cube complex. In addition, if G is also
word-hyperbolic (i.e., if G contains no Baumslag-Solitar subgroups of any
type), we show that G is linear (in fact, is a subgroup of
SLn(Z)).
- (with I. J. Leary) Artin HNN-extensions virtually embed in Artin
groups, Bull. Lon. Math. Soc. 40 (2008), no. 4, 715-719.
An Artin HNN-extension is an HNN-extension of an Artin group
in which the stable letter conjugates a pair of suitably chosen subsets of
the standard generating set. We show that some finite index subgroup of an
Artin HNN-extension embeds in an Artin group. We also obtain an analogous
result for Coxeter groups. (Download at
LMS)
- (with D. T. Wise) Groups with infinitely many types of fixed subgroups,
Israel J. Math. 144 (2004), 93-107.
It is a theorem of Shor that if G is a word-hyperbolic
group, then up to isomorphism, only finitely many groups appear as fixed
subgroups of automorphisms of G. We give an example of a group G acting
freely and cocompactly on a CAT(0) square complex such that infinitely many
non-isomorphic groups appear as fixed subgroups of automorphisms of G.
Consequently, Shor's finiteness result does not hold if the negative
curvature condition is relaxed to either biautomaticity or nonpositive
curvature. (pdf version) (ps
version)
- (with D. T. Wise) Ascending HNN extensions of polycyclic groups are
residually finite, J. Pure Appl. Alg. 182 (2003), no. 1, 65-78.
We prove that every ascending HNN extension of a
polycyclic-by-finite group is residually finite. We also give a criterion for
the residual finiteness of an ascending HNN extension of a residually
nilpotent group, and apply this criterion to recover a result of Sapir on the
residual finiteness of certain ascending HNN extensions of free groups.
(pdf version) (ps
version)
- (with D. T. Wise) Separating quasiconvex subgroups of right-angled
Artin groups, Math. Z. 240 (2002), no. 3, 521-548.
A graph group, or right-angled Artin group, is a
group given by a presentation where the only relators are commutators of the
generators. A graph group presentation corresponds in a natural way to a
simplicial graph, with each generator corresponding to a vertex, and each
commutator relator corresponding to an edge. We show that if H is a
quasiconvex subgroup of a right-angled Artin group G whose corresponding
graph is a tree, then H is a separable subgroup of G, or in other
words, H is the intersection of finite index subgroups of G. We also
discuss some consequences relating to knot groups and 3-manifolds.
(pdf version) (ps
version)
- (with D. T. Wise) On linear and residual properties of graph products,
Mich. Math. J. 46 (1999), 251-259.
If
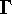 is a
graph, and Gv is a set of groups indexed by the vertices of
is a
graph, and Gv is a set of groups indexed by the vertices of
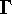 , then the graph
product G
, then the graph
product G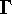 is defined
to be the free product of the Gv, modulo the relations [gv,gw]=1 for
all gv in Gv and gw in Gw such that (v,w) is an edge in
is defined
to be the free product of the Gv, modulo the relations [gv,gw]=1 for
all gv in Gv and gw in Gw such that (v,w) is an edge in
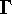 . We show that the graph
product of subgroups of Coxeter groups is a subgroup of a Coxeter group. As a
result, we obtain short proofs that graph groups (right-angled Artin groups)
are linear and that the graph product of residually finite groups is
residually finite. We also give a new and more geometric proof of the normal
form theorem for graph products. (pdf version)
(ps version)
. We show that the graph
product of subgroups of Coxeter groups is a subgroup of a Coxeter group. As a
result, we obtain short proofs that graph groups (right-angled Artin groups)
are linear and that the graph product of residually finite groups is
residually finite. We also give a new and more geometric proof of the normal
form theorem for graph products. (pdf version)
(ps version)
- (with D. T. Wise) A non-residually finite square of finite groups, in
C. M. Campbell et al. (eds.), Groups St. Andrews 1997 in Bath, I,
volume 260 of LMS Lect. Notes, 368-378. Cambridge Univ. Press,
1999.
We construct a non-positively curved non-residually finite
square of finite groups whose vertex groups are of order 288, 288, 576, and
576. (In contrast, the example constructed in [10] has vertex
groups of order between 260 and 2150.) In doing so, we demonstrate
a new, more geometric method for embedding the fundamental group of a
complete squared complex in the fundamental group of a square of finite
groups. (pdf version) (ps
version)
- (with D. T. Wise) Embedding theorems for non-positively curved polygons
of finite groups, J. Pure Appl. Alg. 123 (1998), 201-221.
The fundamental groups of complete squared complexes are a
class of groups, some of which are not residually finite. A method is given
for embedding the fundamental group of a complete squared complex as a
subgroup of a square of finite groups, all of whose (Gersten-Stallings)
vertex angles are <=
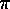 /2.
It is also shown that every square of finite groups, all of whose vertex
angles are <=
/2.
It is also shown that every square of finite groups, all of whose vertex
angles are <= 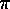 /2 can be
embedded in a non-positively curved triangle of finite groups. In this way, a
non-residually finite, non-positively curved triangle of finite groups is
obtained. (pdf version) (ps
version)
/2 can be
embedded in a non-positively curved triangle of finite groups. In this way, a
non-residually finite, non-positively curved triangle of finite groups is
obtained. (pdf version) (ps
version)
Combinatorics of partially ordered sets
- (with C. Petersen) Upset-downset, In preparation, 2017.
- (with C. Day) Blue-red CHOMP, In preparation, 2017.
- (with M. J. Logan and S. Shahriari) Methods for nesting rank 3 normalized
matching rank-unimodal posets, Disc. Math. 309 (2009), no. 3,
521-531.
Anderson and Griggs proved independently that a rank-symmetric-unimodal
normalized matching (NM) poset possesses a nested chain decomposition (or
nesting), and Griggs later conjectured that this result still holds
if we remove the condition of rank-symmetry. We give several methods for
constructing nestings of rank-unimodal NM posets of rank 3, which together
produce substantial progress towards the rank 3 case of the Griggs nesting
conjecture. In particular, we show that certain nearly symmetric posets are
nested; we show that certain highly asymmetric rank 3 NM posets are nested;
and we use results on minimal rank 1 NM posets to show that certain other
rank 3 NM posets are nested.
- (with M. J. Logan and S. Shahriari) The generalized Füredi
conjecture holds for finite linear lattices, Disc. Math. 306 (2006),
3140-3144.
We define an Anderson-Griggs poset to be a finite rank-unimodal,
rank-symmetric, normalized matching poset P, and we say that P has rapidly decreasing rank numbers if below the largest ranks in the middle
of P, the size of each level is at most half of the previous one.
Generalizing a question of Füredi about the Boolean lattice, we
conjecture that every Anderson-Griggs poset of width w has a partition into
w chains such that the size of each chain is one of two consecutive
integers. We prove the conjecture for all Anderson-Griggs posets with rank
<= 3, and consequently obtain the conjecture for Anderson-Griggs posets
with rapidly decreasing rank numbers. In particular, there exists a partition
of the linear lattice Ln(q) (subspaces of an n-dimensional vector space
over a field of order q, ordered by inclusion) into chains such that the
number of chains is the number of subspaces of dimension
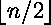 , and the size of
each chain is one of two consecutive integers. (pdf
version) (ps version)
, and the size of
each chain is one of two consecutive integers. (pdf
version) (ps version)
- (with M. J. Logan, S. Shahriari, and C. Towse) Partitioning the Boolean
lattice into a minimal number of chains of relatively uniform size, Eur. J.
Comb. 24 (2003), no. 2, 219-228.
Let 2[n] denote the Boolean lattice of order n, that
is, the poset of subsets of {1,...,n} ordered by inclusion. Extending
our previous work on a question of Füredi, we show that for any c>1,
there exist functions e(n)~sqrt(n)/2 and f(n)~csqrt(nlogn) and
an integer N (depending only on c) such that for all n>N, there is a
chain decomposition of the Boolean lattice 2[n] into
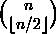 chains,
all of which have size between e(n) and f(n). (A positive answer to
Füredi's question would imply that the same result holds for some
e(n)~sqrt(pi/2)sqrt(n) and f(n)=e(n)+1.) The main tool used is a
matching property of normalized matching posets that is not hard to prove,
but does not seem to have been widely used before. (pdf
version) (ps
version)
chains,
all of which have size between e(n) and f(n). (A positive answer to
Füredi's question would imply that the same result holds for some
e(n)~sqrt(pi/2)sqrt(n) and f(n)=e(n)+1.) The main tool used is a
matching property of normalized matching posets that is not hard to prove,
but does not seem to have been widely used before. (pdf
version) (ps
version)
- (with M. J. Logan, S. Shahriari, and C. Towse) Partitioning the Boolean
lattice into chains of large minimum size, J. Comb. Thy. (A) 97
(2002), no. 1, 62-84.
Let 2[n] denote the Boolean lattice of order n, that
is, the poset of subsets of {1,...,n} ordered by inclusion. Recall
that 2[n] may be partitioned into what we call the canonical symmetric chain decomposition (due to de Bruijn, Tengbergen, and
Kruyswijk), or CSCD. Motivated by a question of Füredi, we show that
there exists a function d(n)~(1/2) sqrt(n) such that for any n >= 0,
2[n] may be partitioned into
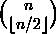 chains of
size at least d(n). (For comparison, a positive answer to Füredi's
question would imply that the same result holds for some d(n)~sqrt(pi/2)sqrt(n).) More precisely, we first show that for 0 <= j <= n,
the union of the lowest j+1 elements from each of the chains in the CSCD of
2[n] forms a poset Tj(n) with the normalized
matching property and log-concave rank numbers. We then use our results on
Tj(n) to show that the nodes in the CSCD chains of size less than
2d(n) may be repartitioned into chains of large minimum size, as desired.
(pdf version) (ps
version)
chains of
size at least d(n). (For comparison, a positive answer to Füredi's
question would imply that the same result holds for some d(n)~sqrt(pi/2)sqrt(n).) More precisely, we first show that for 0 <= j <= n,
the union of the lowest j+1 elements from each of the chains in the CSCD of
2[n] forms a poset Tj(n) with the normalized
matching property and log-concave rank numbers. We then use our results on
Tj(n) to show that the nodes in the CSCD chains of size less than
2d(n) may be repartitioned into chains of large minimum size, as desired.
(pdf version) (ps
version)
Expository articles
- Rational nonaxis points on the unit circle have irrational angles, Amer.
Math. Monthly 123 (2016), no. 5, 490.
We give a short elementary proof that any rational point on
the unit circle that does not lie on a coordinate axis has an angle that is
an irrational multiple of pi.
- (with J. H. Conway) Some very interesting sequences, in T. Shubin, D. F.
Hayes, and G. Alexanderson (eds.), Expeditions in Mathematics, MAA
Spectrum series, chapter 6, 75-86. MAA, Washington, DC, 2011.
In this expository paper, aimed at talented high school
students and mathematical enthusiasts of all ages, we discuss a few of our
favorite sequences and their remarkable properties. Topics include the
Fibonacci sequence, the FRACTRAN program for primes, the omnipresent
Bernoulli numbers, and many others. (pdf
version) (ps
version)
Moufang loops
- Explicit constructions of code loops as centrally twisted products,
Math. Proc. Camb. Phil. Soc. 128 (2000), 223-232.
Code loops are certain Moufang loop extensions of
doubly even binary codes that have many applications in finite group theory
(e.g., Conway's construction of the Monster). We give several methods for
explicitly constructing code loops as centrally twisted products. More
specifically, after establishing some preliminary examples, we show how to
use decompositions of codes, such as Turyn's construction of the Golay code
or the decomposition of a cyclic code into minimal cyclic codes, to build
code loops out of more familiar pieces, such as abelian groups, extraspecial
groups, or the octonion loop. (pdf version)
(ps version)
- Moufang loops of class 2 and cubic forms, Math. Proc. Camb. Phil.
Soc. 128 (2000), 197-222.
Let L be a Moufang loop that is centrally nilpotent of class
2. We first show that the nuclearly-derived subloop (normal associator
subloop) L* of L has exponent dividing 6. It follows that Lp (the
subloop of L of elements of p-power order) is associative for p>3.
Next, a Moufang loop L is said to be a small Frattini Moufang loop,
or SFML, if L has a central subgroup Z of order p such that L/Z is an
elementary abelian p-group. (For instance, it follows from work of Chein
and Goodaire that the SFM 2-loops are precisely the class of code
loops, in the sense of Griess.) L/Z is thus given the structure of what we
call a coded vector space, or CVS. (For p>2, a CVS is a vector space
with attached linear, bilinear, and trilinear forms, and for p=2, a CVS is
a vector space equipped with functions that act like the intersection
structure of a doubly even binary code.) We show that every CVS may be
obtained from an SFML in this way, and that two SFML's are isomorphic in a
manner preserving the central subgroup Z if and only if their CVS's are
isomorphic up to scalar multiple. Consequently, we also obtain a relatively
explicit characterization of isotopy in SFM 3-loops, a characterization
easily extended to Moufang loops of class 2 and exponent 3. Finally, we
sketch a method for constructing any finite Moufang loop which is centrally
nilpotent of class 2. (pdf version) (ps
version)
Coset representations of modular subgroups
- Permutation techniques for coset representations of modular subgroups,
in L. Schneps (ed.), Geometric Galois Actions II: Dessins
d'Enfants, Mapping Class Groups and Moduli, volume 243 of LMS Lect.
Notes, 67-77. Cambridge Univ. Press, 1997.
This article surveys the use of coset representations
(specifying a subgroup G1<G by writing down the action of G on the
cosets of G1 in G) in working with dessins d'enfants and similar
structures. Questions expressed in terms of subgroups may sometimes be solved
more easily in terms of coset representations. For instance, the results of
[22] are summarized and then extended to obtain algorithms for
solving problems such as finding the congruence closure of a modular
subgroup. (pdf version) (ps
version)
- Identifying congruence subgroups of the modular group, Proc. AMS 124 (1996), no. 5, 1351-1359.
A simple test for determining if a given subgroup of
PSL2(Z) is a congruence subgroup is exhibited, and a detailed description
of its implementation is given. A more "invariant" congruence test is also
described. (pdf version) (ps
version)
Quilts
- Quilts: Central extensions, braid actions, and finite groups, volume
1731 of Lect. Notes Math., Springer-Verlag, 2000.
Quilts (developed by Norton, Parker, Conway, and the author)
are 2-complexes used to analyze actions and subgroups of the 3-string braid
group and similar groups. This research monograph, which supersedes
[26] and [27], establishes the fundamentals of
quilts and discusses connections with central extensions, braid actions, and
finite groups, especially in the context of the Monstrous Moonshine
phenomenon. In particular, Norton's action of the 3-string braid
group on pairs of elements (resp. triples of involutions) of a finite group
is analyzed in detail; new results on central extensions of triangle groups,
triangle group quotients, and covers of Seifert fibered 3-manifolds are
discussed; several open questions from [26] are resolved; and some
open problems are discussed. (at
Springer-Verlag)
(at
amazon.com)
- Quilts, the 3-string braid group, and braid actions on finite groups: an
introduction, in J. Ferrar and K. Harada (eds.), The Monster and
Lie Algebras, volume 7 of Ohio State Univ. Math. Res. Inst.
Pubs., 85-97. de Gruyter, 1998.
This article gives a brief introduction to the basic
definitions and results on quilts (fully described in [23]). In
particular, we show how quilts may be used to study Norton's action of B3
on pairs of elements (resp. triples of involutions) of a finite group, which
may be relevant to the Generalized Moonshine conjectures, and we work out
some small examples. (ps version)
- Some quilts for the Mathieu groups, in C. Dong and G. Mason (eds.),
Moonshine, the Monster, and Related Topics, volume 193 of Contemp. Math., 113-122. AMS, 1996.
Examples of quilts arising from the Mathieu groups are
presented, and some associated presentations are examined. In particular,
presentations for some interesting extensions of M11, M12, and
M21=L3(4) are exhibited. (ps
version)
- Quilts, T-systems, and the combinatorics of Fuchsian groups, PhD
thesis, Princeton Univ., 1994.
- (with J. H. Conway) Quilts and T-systems, J. Alg. 174 (1995),
856-908.
tim.hsu@sjsu.edu
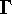 is a
graph, and Gv is a set of groups indexed by the vertices of
is a
graph, and Gv is a set of groups indexed by the vertices of
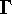 , then the graph
product G
, then the graph
product G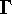 is defined
to be the free product of the Gv, modulo the relations [gv,gw]=1 for
all gv in Gv and gw in Gw such that (v,w) is an edge in
is defined
to be the free product of the Gv, modulo the relations [gv,gw]=1 for
all gv in Gv and gw in Gw such that (v,w) is an edge in
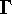 . We show that the graph
product of subgroups of Coxeter groups is a subgroup of a Coxeter group. As a
result, we obtain short proofs that graph groups (right-angled Artin groups)
are linear and that the graph product of residually finite groups is
residually finite. We also give a new and more geometric proof of the normal
form theorem for graph products. (pdf version)
(ps version)
. We show that the graph
product of subgroups of Coxeter groups is a subgroup of a Coxeter group. As a
result, we obtain short proofs that graph groups (right-angled Artin groups)
are linear and that the graph product of residually finite groups is
residually finite. We also give a new and more geometric proof of the normal
form theorem for graph products. (pdf version)
(ps version)
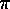 /2.
It is also shown that every square of finite groups, all of whose vertex
angles are <=
/2.
It is also shown that every square of finite groups, all of whose vertex
angles are <= 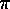 /2 can be
embedded in a non-positively curved triangle of finite groups. In this way, a
non-residually finite, non-positively curved triangle of finite groups is
obtained. (pdf version) (ps
version)
/2 can be
embedded in a non-positively curved triangle of finite groups. In this way, a
non-residually finite, non-positively curved triangle of finite groups is
obtained. (pdf version) (ps
version)
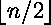 , and the size of
each chain is one of two consecutive integers. (pdf
version) (ps version)
, and the size of
each chain is one of two consecutive integers. (pdf
version) (ps version)
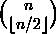 chains,
all of which have size between e(n) and f(n). (A positive answer to
Füredi's question would imply that the same result holds for some
e(n)~sqrt(pi/2)sqrt(n) and f(n)=e(n)+1.) The main tool used is a
matching property of normalized matching posets that is not hard to prove,
but does not seem to have been widely used before. (pdf
version) (ps
version)
chains,
all of which have size between e(n) and f(n). (A positive answer to
Füredi's question would imply that the same result holds for some
e(n)~sqrt(pi/2)sqrt(n) and f(n)=e(n)+1.) The main tool used is a
matching property of normalized matching posets that is not hard to prove,
but does not seem to have been widely used before. (pdf
version) (ps
version)
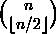 chains of
size at least d(n). (For comparison, a positive answer to Füredi's
question would imply that the same result holds for some d(n)~sqrt(pi/2)sqrt(n).) More precisely, we first show that for 0 <= j <= n,
the union of the lowest j+1 elements from each of the chains in the CSCD of
2[n] forms a poset Tj(n) with the normalized
matching property and log-concave rank numbers. We then use our results on
Tj(n) to show that the nodes in the CSCD chains of size less than
2d(n) may be repartitioned into chains of large minimum size, as desired.
(pdf version) (ps
version)
chains of
size at least d(n). (For comparison, a positive answer to Füredi's
question would imply that the same result holds for some d(n)~sqrt(pi/2)sqrt(n).) More precisely, we first show that for 0 <= j <= n,
the union of the lowest j+1 elements from each of the chains in the CSCD of
2[n] forms a poset Tj(n) with the normalized
matching property and log-concave rank numbers. We then use our results on
Tj(n) to show that the nodes in the CSCD chains of size less than
2d(n) may be repartitioned into chains of large minimum size, as desired.
(pdf version) (ps
version)